Ecuación de la recta y demases III...

En esta entrada se abordarán las distintas formas de la ecuación de la recta y su aplicación, además de la ecuación punto-pendiente.

En primer lugar, recordar que la ecuación de la recta está asociada a la función afín, es decir a la función de la forma f(x) = mx + n ; donde m corresponde a la pendiente y n corresponde al coeficiente de posición. Existen tres formas de representar la ecuación de la recta y cada una de ellas, nos permite calcular algunos elementos de manera más rápida que otra, por ejemplo.

Ecuación principal

Corresponde a la ecuación de la función afín, es decir:

y = mx + n ; con m como la pendiente y n como el coeficiente de posición. La ventaja que tiene esta fórmula es que se pueden obtener distintos valores de y, dependiendo de x de manera sencilla. Por ejemplo: y = 2x +6  podemos obtener distintos valores de y dependiendo de cuanto valga x, esto es útil, cuando debemos dibujar la recta en el plano. En este caso seleccionamos dos puntos y los unimos para obtener la recta que representa la ecuación. Seleccionaremos las coordenadas 2 y 3 en el eje X, por lo cual, aplicando la ecuación principal, obtenemos las coordenadas 10 y 12 para el eje Y respectivamente. Así, ahora tenemos dos puntos, P(2, 10) y P'(3, 12).


Ecuación general
Corresponde a la ecuación de la forma Ax + By + C = 0 y es una variación de la ecuación principal. Suele utilizarse en los sistemas de ecuaciones con la forma Ax + By = C. En esta ecuación podemos deducir la pendiente con la fórmula -A/B y al coeficiente de posición con la fórmula -C/B.
Ejemplo:
A partir de la recta L: 3x + 3y - 10 = 0, determine:
- Pendiente de la recta
- Coeficiente de posición
- Ecuación principal de la recta
Pendiente de la recta
Se utiliza la expresión -A/B , por lo tanto: -3/3 = -1 , por lo cual, m = -1
Coeficiente de posición
Se usa la expresión -C/B , por lo tanto: - (-10/3) = 10/3 , por lo cual, n = 10/3
Ecuación principal
Se tiene la pendiente y el coeficiente de posición, por lo tanto se escribe como 

y = -x + 10/3

Ecuación canónica

Se utiliza para determinar la ecuación de la recta utilizando como referencia las intersecciones con los ejes del plano cartesiano (X e Y).

Se expresa como: x/p + y/q = 1 donde p es la intersección con el eje X y q es la intersección con el eje Y.

Ejemplo:

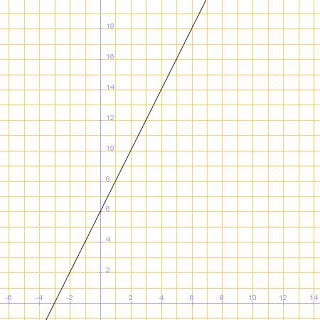
A partir de la siguiente recta, determine la ecuación canónica y principal de la recta.

Se determinan los puntos de intersección, para el eje X corresponde al punto (-3 , 0) y para el eje Y corresponde al punto (3, 0). Entonces, la ecuación canónica sería:

-x/3 + y/3 = 1

A partir de la misma se puede determinar la ecuación principal, se multiplica por 3 y queda: -x + y = 3 , se pasa la x al otro lado y queda la expresión:

y = x + 3

Se comprueba que verdaderamente corresponde a la ecuación principal de la recta.